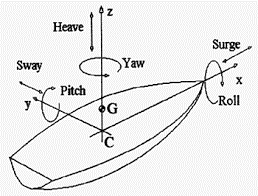
A ship has available to it motion in three axes. Motion on the “X” axis is roll, motion on the “Y” axis is pitch, and motion on the “Z axis is yaw.
This diagram adds “surge,” and “heave,” but they are a bit beyond the scope of the question.
The first question is to directional stability, or stability in “Yaw.” This stability is attained in a similar way to the feathers on an arrow, by the greater resistance to motion at the aft end of the vessel, affected by the trim, or difference in draught forwards to aft, and controlled by the rudder.
There are 3 types of motions stability:
1. Straight line stability:
This is the ships ability to resume a straight-line path without application of control surface forces.
This means, if the ship takes a straight-line path after the disturbance is removed, then it is said to possess straight-line stability.
2. Directional stability:
This is the ship’s ability to resume a straight line path having the same direction as it had before the disturbance.
There can be two possible paths during the disturbance phase: either it can be oscillatory or non-oscillatory.
3. Positional stability: 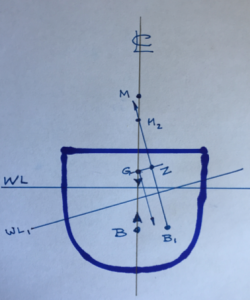
This is the ship’s ability to resume a straight line path having the same direction and position it had before the disturbance.
Here by position we mean that it follows essentially the same straight line path it had before the disturbance.
A ship is said to be directionally stable if a deviation from a set course increases only while an external force or moment is acting to cause the deviation. On the other hand, it is said to be unstable if a course deviation begins or continues even in the absence of an external cause. A directionally unstable ship is easy to maneuver, while a stable ship requires less energy expenditure by its steering gear in maintaining a set course. A compromise between extremes is therefore desirable. In a rough sense, directional stability or instability can be determined by examination of the ship’s underwater profile. If the area of the hull and its appendages is concentrated toward the aft end, then the ship is likely to be directionally stable.
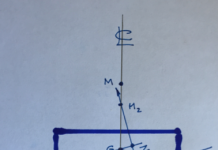
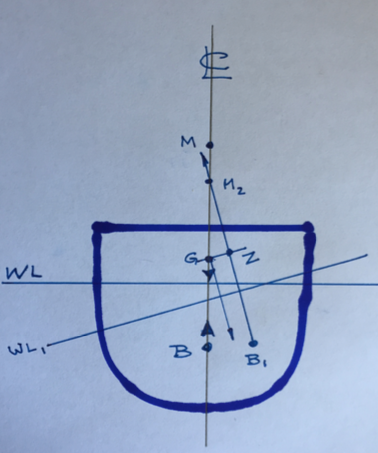
Dynamic stability refers to the vessels ability to resist forces in the “X” axis, or roll. This is controlled by the basic shape of the hull, and the location of the weights, cargo, machinery, and equipment within the hull. On the diagram, these are presumed to act at the point “G.”
“B,” the point through which all the buoyant forces act, and “M,” the metacentre, the point on the centreline through which buoyancy acts, a point that moves as the vessel heels when acted on by an outside force.
The effect of the basic shape of the ship comes into this through the relationship BM = I / V, where “I” is the moment of inertia of the water plane, a basic function of the hull form, and “V” is the volume of displacement.
We now know the distance from the centre of buoyancy to the metacentre. Back to dynamic stability.
But it is easy to see the shift in “M” as the ship rolls. If the ship rolls far enough, “M” will go below “G” which is a fixed point.
Until then, the distance GZ acts as a lever resisting the roll, and attempts to restore the ship to upright. As the ship rolls, there comes a point where the lever diminishes, finally becoming negative.
At that point the ship rolls over.
Courtsey- C/E Nilesh Ambokar